
Сайт преподавателя
математики и информатики
математики и информатики

Главная |
Познакомимся |
Методическая копилка |
Внеклассная деятельность |
Фотогалерея |
Наше творчество |
|
Олимпиадные задания Олимпиадные задания для 5 классаОлимпиадные задания для 6 классаОлимпиадные задания для 7 классаОлимпиадные задания для 8 классаОлимпиадные задания для 9 классаОлимпиадные задания для 5 класса - 2008 год- 1) Расставьте скобки всеми возможными способами; выберите наибольший и наименьший результат: 100-20*3+2 (2б) 2) В мешке 24 кг гвоздей. Как имея только чашечные весы без гирь, отмерить 9 кг гвоздей? (6б) 3) Как из восьмилитрового ведра с молоком отлить один литр с помощью трёхлитровой банки и пятилитрового бидона? (6б) 4) Как круг разделить тремя прямыми на 4, 5, 6, 7 частей? (9б) 5) В семье четверо детей, им 5, 8, 13 и 15 лет. Детей зовут Аня, Боря, Вера, Галя. Сколько лет каждому ребёнку, если одна девочка ходит в детский сад, Аня старше Бори и сумма лет Ани и Веры делится на 3? (9б) |
|
Олимпиадные задания для 6 класса - 2008 год- 1) В записи 52*2* замените звёздочки цифрами так, чтобы полученное число делилось на 36. Укажите все возможные решения. (6б) 2) В коробке лежат 7 красных и 5 синих карандашей. В темноте из коробки берут карандаши. Сколько надо взять карандашей, чтобы среди них было не менее 2 красных и 3 синих? (6б) 3) Длину прямоугольного участка увеличили на 35%, а ширину уменьшили на 14%. На сколько процентов изменилась площадь участка? (6б) 4) Переложите одну из семи спичек, изображающих число 7/10 записанное римскими цифрами (т.е.VII/X) так, чтобы получившаяся дробь равнялась 2/3. (9б) 5) Барон Мюнхгаузен утверждал, что ему удалось найти натуральное число, произведение всех цифр которого 208. Докажите, что барон ошибся.(9б) Олимпиадные задания для 7 класса - 2008 год- 1) При каких значениях с уравнение сх = 9 2) Сократите дробь: 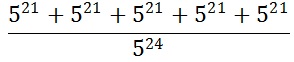 (7б) (7б)3) Один фонтан наполняет бассейн за 2,5 часа, а другой за 3,75 часа. За какое время наполнят бассейн оба фонтана? (5б) 4) Бочка наполнена бензином. Как перелить из неё в мотоцикл 6 л бензина с помощью 9-литрового ведра и 5-литрового бидона? (7б) 5) Разрежьте квадрат на 5 прямоугольников так, чтобы у соседних прямоугольников стороны не совпали. (5б) Олимпиадные задания для 8 класса - 2008 год- 1) Упростите выражение: 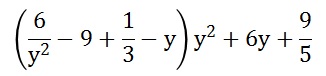 (5б) (5б)2) Какой треугольник надо взять, чтобы после проведения в нём одного отрезка получить все известные виды треугольников: равносторонний, равнобедренный, разносторонний, прямоугольный, остроугольный, тупоугольный. (6б) 3) Построить график функции: 4) Число 19 представить в виде разности кубов натуральных чисел. Показать, что такое представление единственно. (9б) 5) Две шкурки общей стоимостью 2250 рублей были проданы на аукционе с прибылью в 40%. Какова стоимость каждой шкурки, если от первой было получено прибыли 25%, а от второй 50%. (9б) Олимпиадные задания для 9 класса - 2008 год- 1) Постройте график функции: 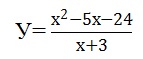 (5б) (5б)2) Зная, что 1993 простое число, решите уравнение х3-у3=1993 в натуральных числах.(7б) 3) Четверо ребят - Алексей, Борис, Владимир и Григорий участвовали в лыжных гонках. На следующий день, на вопром кто какое место занял, они ответили так: Алексей: "Я не был ни первым и не последним"; Борис: "Я не был последним"; Владимир: "Я был первым"; Григорий: "Я был последним". Известно, что три из этих ответов были правдивыми, а один ложью. Кто сказал правду? Кто был первым? (6б) 4) Известно, что а+в+с=5, ав+ас+вс=5. Чему может равняться а2+в2+с2 (8б) 5) Две окружности радиусами 3 см и 1 см касаются внешним образом. Найти расстояние от точки касания до общей касательной, проведённой к этим окружностям. (9б) |