Алгебра |
Методическая копилка |
Корни и степени |
|
Занятие 1 . |
Понятие корня n-ой степени из действительного числа. |
Занятие 2 |
Свойства корня n-ой степени. |
Занятие 3 |
Свойства корня n-ой степени. |
Логарифмы |
|
Занятие 4 |
Понятие логарифма.Свойства логарифмов. |
Занятие 5 |
Свойства логарифмов. |
Занятие 6 |
Свойства логарифмов. |
Занятие 7 |
Переход к новому основанию логарифма. |
Занятие 8 |
Преобразование логарифмических выражений. |
Основные понятия Основные тригонометрические тождества |
|
Занятие 9 |
Числовая окружность. Синус и косинус. Тангенс и котангенс. |
Занятие 10 |
Тригонометрические функции числового и углового аргументов. Формулы приведения. |
Преобразования простейших тригонометрических выражений |
|
Занятие 11 |
Синус, косинус и тангенс суммы и разности аргументов. |
Занятие 12 |
Формулы двойного аргумента. |
Занятие 13 |
Преобразование сумм тригонометрических функций в произведение. |
Занятие 14 |
Преобразование тригонометрических выражений. |
Тригонометрические уравнения и неравенства |
|
Занятие 15 |
Решение тригонометрических уравнений. |
Занятие 16 |
Решение тригонометрических уравнений. |
Занятие 17 |
Решение тригонометрических неравенств. |
Занятие 18 |
Решение тригонометрических неравенств. |
Свойства функций |
|
Занятие 19 |
Свойства функций. |
Степенные функции |
|
Занятие 20 |
Степенные функции их свойства и графики. |
Занятие 21 |
Степенные функции их свойства и графики. |
Показательная функция |
|
Занятие 22 |
Показательная функция её свойства и график. |
Занятие 23 |
Показательная функция её свойства и график. |
Логарифмическая функция |
|
Занятие 24 |
Логарифмическая функция её свойства и график. |
Занятие 25 |
Логарифмическая функция её свойства и график. |
Тригонометрические функции |
|
Занятие 26 |
Функции y=sinx, y=cosx, их свойства и графики. |
Занятие 27 |
Функции y=tgx, y=ctgx, их свойства и графики. |
Занятие 28 |
Преобразование графиков тригонометрических функций. |
Уравнения и системы уравнений |
|
Занятие 29 |
Показательные уравнения. |
Занятие 30 |
Логарифмические уравнения. |
Занятие 31 |
Уравнения и системы уравнений. |
Неравенства |
|
Занятие 32 |
Неравенства. |
Занятие 33 |
Показательные неравенства. |
Занятие 34 |
Логарифмические неравенства. |
Предел числовой последовательности |
|
Занятие 35 |
Числовые последовательности. Предел числовой последовательности. |
Производная функций |
|
Занятие 36 |
Вычисление производных. |
Занятие 37 |
Производная сложной функции. |
Занятие 38 |
Уравнение касательной к графику. |
Занятие 39 |
Применение производной для исследования функций на монотонность и экстремумы. |
Занятие 40 |
Применение производной для отыскания наибольших и наименьших значений. |
Первообразная и интеграл |
|
Занятие 41 |
Первообразная и неопределённый интеграл. |
Занятие 42 |
Определённый интеграл. |
Занятие 43 |
Определённый интеграл. |
Занятие 44 |
Применение определённого интеграла к вычислению площадей плоских фигур. |
Занятие 45 |
Применение определённого интеграла к вычислению площадей плоских фигур. |
Элементы комбинаторики |
|
Занятие 46 |
Случайные события. Вероятность событий. |
Занятие 47 |
Математическая статистика. |
Единичной окружностью называют окружность радиуса 1.
Числовая окружность - это единичная окружность, точки которой соответствуют определенным действительным числам.
Отсчет по числовой окружности может вестись как по часовой стрелке, так и против часовой стрелки.
Отсчет от точки А против часовой стрелки называется положительным направлением.
Отсчет от точки А по часовой стрелке называется отрицательным направлением.
Центр радиуса числовой окружности соответствует началу координат (числу 0).
Горизонтальный диаметр соответствует оси x, вертикальный - оси y.
Начальная точка А числовой окружности находится на оси x и имеет координаты (1; 0).
Любая точка числовой окружности с координатами (x; y) не может быть меньше -1, но не может быть больше 1:
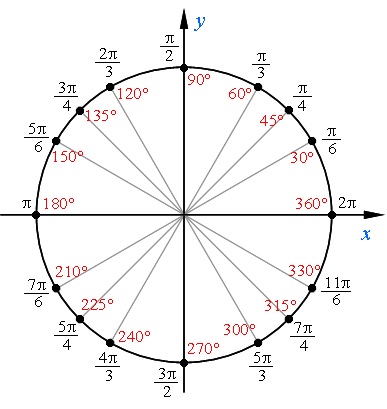
Есть несколько простых закономерностей, которые помогут вам легко запомнить основные имена числовой окружности.
Перед тем как начать, напомним: отсчет ведется в положительном направлении, то есть от точки А (2П) против часовой стрелки.
1) Начнем с крайних точек на осях координат.
Начальная точка - это 2П (крайняя правая точка на оси х, равная 1).
Как вы знаете, 2П - это длина окружности. Значит, половина окружности - это 1П или П. Ось х делит окружность как раз пополам.
Соответственно, крайняя левая точка на оси х, равная -1, называется П.
Крайняя верхняя точка на оси у, равная 1, делит верхнюю полуокружность пополам. Значит, если полуокружность - это П, то половина полуокружности - это П/2.
Одновременно П/2 - это и четверть окружности. Отсчитаем три таких четверти от первой до третьей - и мы придем в крайнюю нижнюю точку на оси у, равной -1.
Но если она включает три четверти - значит имя ей 3П/2. Определение. Если точка М числовой окружности соответствует числу t, то абсциссу точки М называют
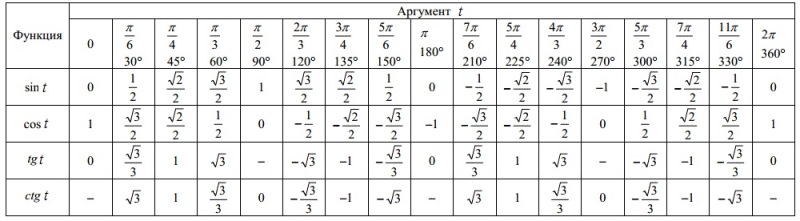
косинусом числа t и обозначают соs t, а ординату точки М называют синусом числа t и обозначают sin t. Определение. Отношение синуса числа t к косинусу того же числа называют тангенсом числа t.
Отношение косинуса числа t к синусу того же числа называют котангенсом числа t.
Равенство, связывающее sin t и соs t: sin2t + cos2t = 1
Свойство 1. cos (-t) = cos(t); sin (-t) = - sin (t); tg (-t) = - tg (t); ctg (-t) = - ctg (t)
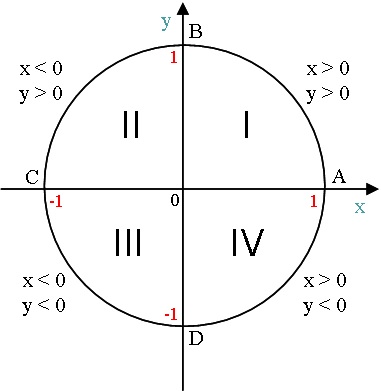
2) Горизонтальный и вертикальный диаметры делят числовую окружность на четыре четверти . Их соответственно называют первой, второй, третьей и четвертой четвертью.
3) Горизонтальный диаметр обозначают AC, причем А - это крайняя правая точка. Вертикальный диаметр обозначают BD, причем B - это крайняя верхняя точка.
первая четверть - это дуга AB
вторая четверть - дуга BC
третья четверть - дуга CD
четвертая четверть - дуга DA
4) Начальная точка числовой окружности - точка А.

![]() ;
; ![]()
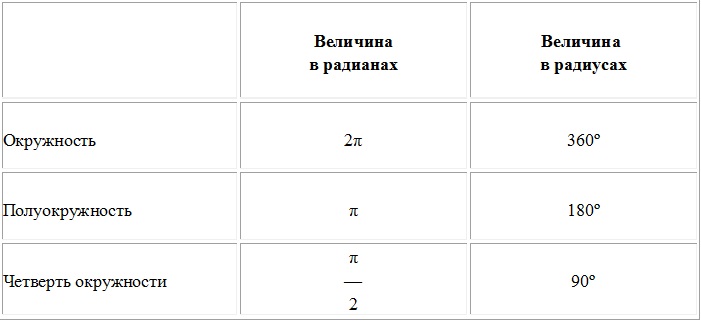
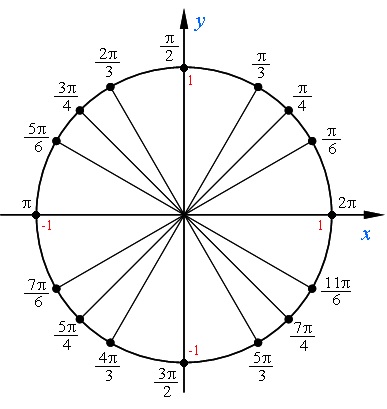
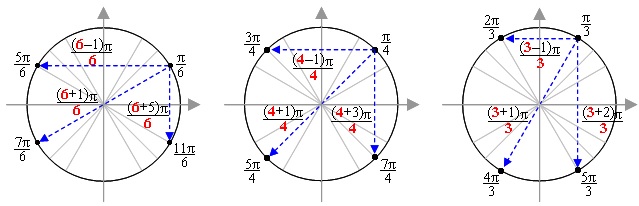
Если М(t) = М(х;у), то х = cost, у = sint.
![]()
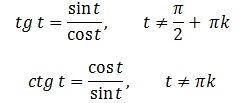
Свойство 2. cos (t+2Пk) = cos (t); sin (t+2Пk) = sin (t); tg (t+2Пk) = tg (t); ctg (t+2Пk) = ctg (t)